What is Going On? Simple Linear Regression

Code 
library(plotly)
library(gganimate)
library(knitr)
library(kableExtra)
library(tidybayes)
library(posterior)
library(bayesplot)
library(cmdstanr)
library(tidyverse)

1 Introduction

The goal of this document is to —. We’ll use Model 5 from the simple linear regression example illustrating program blocks.

1.1 Reference

  • This article is great for showing visualizations in a posterior analysis. I’m drawing extremely heavily from that article for this page, and I highly suggest you read it.
  • bayesplot - a package for visualization of Bayesian models

2 Data

Recall the data is of the form \[ y_i = \alpha + \beta x_i + \epsilon_i, \;\;\;\;\;i = 1, \ldots, n, \tag{1}\]

and we used true values \(\alpha = 2\), \(\beta = 3\), and \(\sigma = 6\) to simulate some data:

Code 
set.seed(4384836)

n <- 30

alpha <- 2
beta <- 3
sigma <- 6

data <- tibble(x = runif(n, 20, 30)) %>% 
  mutate(y = rnorm(n(), alpha + beta*x, sigma))

data %>% 
  ggplot(aes(x = x, y = y)) +
  geom_point()
Figure 1: Raw data

2.1 Statistical Model

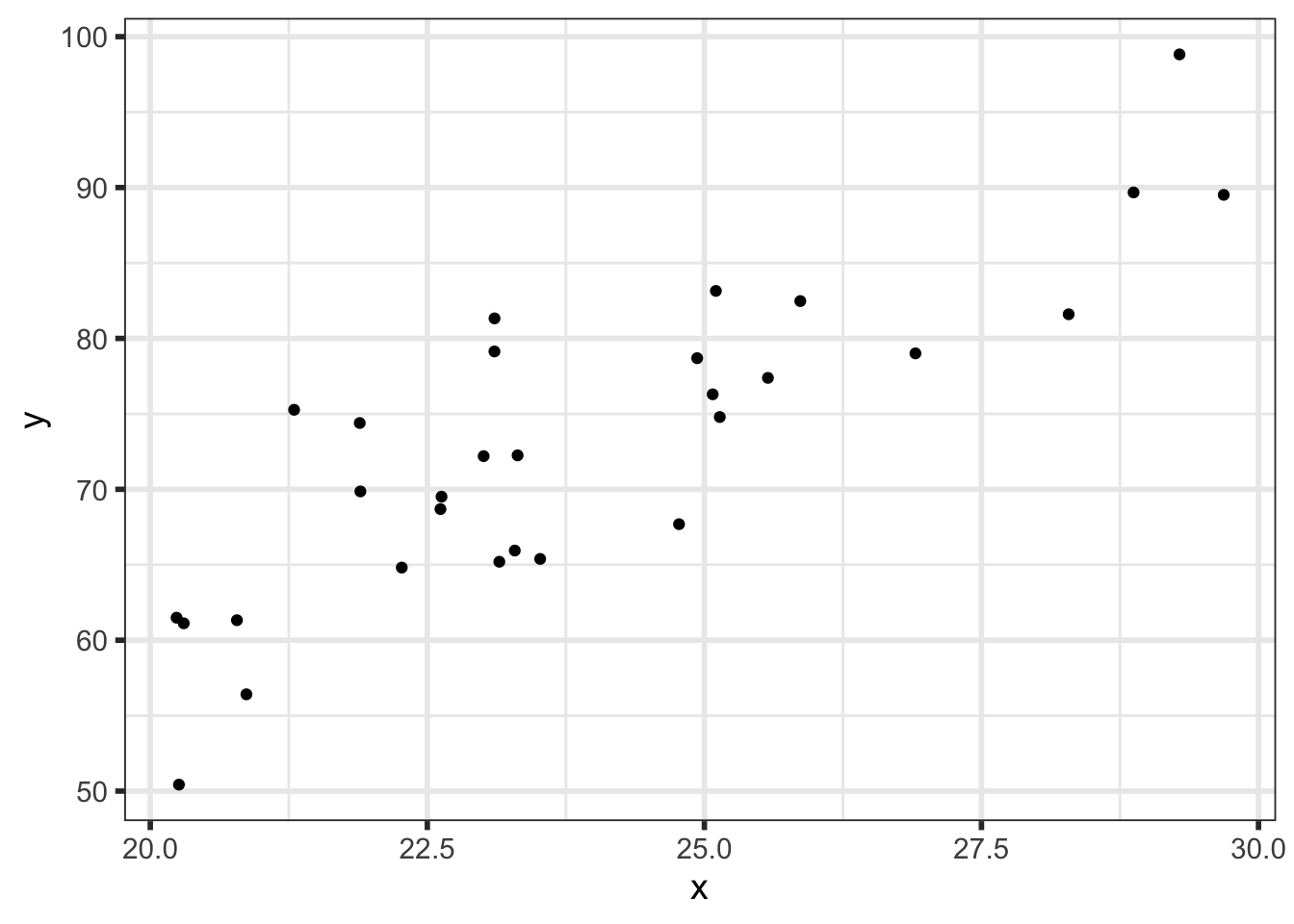
We’ll write down the full statistical model:

\[ \begin{align} Y_i \; | \; \alpha, \beta, \sigma &\sim Normal(\alpha + \beta x_i, \; \sigma) \\ \alpha &\sim Normal(\mu_\alpha, sd_\alpha) \\ \beta &\sim Normal(\mu_\beta, sd_\beta) \\ \sigma &\sim Half-Normal(\mu_\sigma, sd_\sigma) \\ \end{align} \] And we will assume weakly informative priors with hyperparameters as follows:

Table 1: Hyperparameters
Hyperparameter Value
\(\mu_\alpha\) 0
\(sd_\alpha\) 30
\(\mu_\beta\) 0
\(sd_\beta\) 10
\(\mu_\sigma\) 0
\(sd_\sigma\) 15

3 Stan model

Recall the model:

functions{

  vector calculate_mu(real intercept, real slope, vector x){

    vector[num_elements(x)] mu = intercept + slope*x;
    return mu;

  }

}
data{

  int<lower = 1> n;
  array[n] real y;
  vector[n] x;

  real mu_alpha, mu_beta, mu_sigma;
  real<lower = 0> sd_alpha, sd_beta, sd_sigma;

  int<lower = 1> n_pred;
  vector[n_pred] x_pred;

}
parameters{

  real alpha;
  real beta;
  real<lower = 0> sigma;

}
transformed parameters{

  vector[n] mu = calculate_mu(alpha, beta, x);

}
model{

  // Priors
  alpha ~ normal(mu_alpha, sd_alpha);
  beta ~ normal(mu_beta, sd_beta);
  sigma ~ normal(mu_sigma, sd_sigma);

  // Likelihood
  y ~ normal(mu, sigma);

}
generated quantities{

  // PPC - mu is still accessible here, so it doesn't need to be calculated again
  array[n] real y_ppc = normal_rng(mu, sigma);
  
  // Predictions at new points
  vector[n_pred] y_pred_mean = calculate_mu(alpha, beta, x_pred);
  array[n_pred] real y_pred = normal_rng(y_pred_mean, sigma);
  
  // Log-likelihoods of individual observations
  vector[n] log_lik;
  for(i in 1:n){
    log_lik[i] = normal_lpdf(y[i] | mu[i], sigma);
  }

}

4 Fit

Pre-process the data, define your hyperparameters, compile the model, and fit it:

Code 
## model <- cmdstan_model("path/to/your/stan/file.stan")

# New points at which to predict
x_pred <- seq(20, 30, by = 0.1)

stan_data <- list(n = nrow(data),
                  y = data$y,
                  x = data$x,
                  mu_alpha = 0,
                  sd_alpha = 30,
                  mu_beta = 0,
                  sd_beta = 10,
                  mu_sigma = 0,
                  sd_sigma = 15,
                  n_pred = length(x_pred),
                  x_pred = x_pred)

fit <- model$sample(data = stan_data,
                    seed = 112358,
                    chains = 4,
                    parallel_chains = 4,
                    iter_warmup = 1000,
                    iter_sampling = 1000,
                    adapt_delta = 0.8,
                    refresh = 0,
                    max_treedepth = 10)

5 Posterior Summaries

There is an endless amount of analysis we can do with our (samples from the) posterior distribution. Here we will focus on basic posterior summaries of parameters and predictions. Particularly relevant to this section is the bayesplot vignette on plotting MCMC draws.

First, let’s just look at what we have (after wrangling it to get it into a nicer format). The following table shows the actual values for each variable for each draw in our MCMC sample:

Code 
draws_df <- fit$draws(format = "draws_df")

draws_df %>% 
  ungroup() %>% 
  mutate(across(where(is.numeric), \(x) round(x, 3))) %>%
  group_by(.chain) %>% 
  slice_head(n = 10) %>% 
  relocate(starts_with("."), .after = "lp__") %>% 
  DT::datatable()
Table 1
Note

This table shows only the first 10 draws from each chain for readability purposes. There are actually \(4\;(chains) \times 1000 \; (iter\_sampling) = 4000\) draws in our sample.

5.1 Numerical Summaries

We can look at some numerical summaries of the parameters:

Important

We should look at some MCMC diagnostics first, but we’ll just assume everything looks fine for now.

Code 
summary <- summarize_draws(fit$draws(c("alpha", "beta", "sigma")), 
                           mean, median, sd, mcse_mean,
                           ~quantile2(.x, probs = c(0.025, 0.975)), rhat,
                           ess_bulk, ess_tail)

summary %>%
  mutate(rse = sd/mean*100) %>% 
  select(variable, mean, sd, mcse_mean, q2.5, median, q97.5, rse, rhat, 
         starts_with("ess")) %>% 
  mutate(across( -c(rhat, variable), \(x) round(x, 2)), 
         rhat = round(rhat, 3),
         variable = str_c('$\\', variable, '$')) %>%
  knitr::kable(col.names = c("Variable", "Mean", "Std. Dev.", "$MCSE_{mean}$", "2.5%",
                             "Median", "97.5%", "RSE", "$\\hat{R}$", "$ESS_{Bulk}$",
                             "$ESS_{Tail}$"))
Table 2: Numerical summaries
Variable Mean Std. Dev. \(MCSE_{mean}\) 2.5% Median 97.5% RSE \(\hat{R}\) \(ESS_{Bulk}\) \(ESS_{Tail}\)
\(\alpha\) -5.11 9.32 0.29 -23.77 -4.90 13.34 -182.37 1.005 1181.84 767.67
\(\beta\) 3.27 0.39 0.01 2.50 3.27 4.04 11.87 1.005 1212.17 768.00
\(\sigma\) 5.86 0.83 0.02 4.53 5.76 7.76 14.16 1.002 1489.87 1428.21

5.2 Density Plots

Or you can look at density plots of the parameters:

Code 
mcmc_dens(fit$draws(c("alpha", "beta", "sigma")),
          facet_args = list(labeller = ggplot2::label_parsed))
Figure 2: Density plots for the model parameters

5.3 Pairs Plots

Or a pairs plot to see pairwise joint distributions:

Warning

It’s beyond the scope of this page, but notice the high correlation between \(\alpha\) and \(\beta\) and the high uncertainty and MCSE in \(\alpha\) in Table 2. That’s why we centered \(x\) in Model 6 (and for interpretability). You’ll see a much nicer posterior distribution if you fit that one. Try it!

Code 
mcmc_pairs(fit$draws(c("alpha", "beta", "sigma")))

Code 
pairs_plot <- mcmc_pairs(fit$draws(c("alpha", "beta", "sigma")))

pairs_plot$bayesplots[[1]] <- pairs_plot$bayesplots[[1]] + 
  labs(subtitle = latex2exp::TeX("$\\alpha$"))
pairs_plot$bayesplots[[5]] <- pairs_plot$bayesplots[[5]] + 
  labs(subtitle = latex2exp::TeX("$\\beta$"))
pairs_plot$bayesplots[[9]] <- pairs_plot$bayesplots[[9]] + 
  labs(subtitle = latex2exp::TeX("$\\sigma$"))

bayesplot_grid(plots = pairs_plot$bayesplots)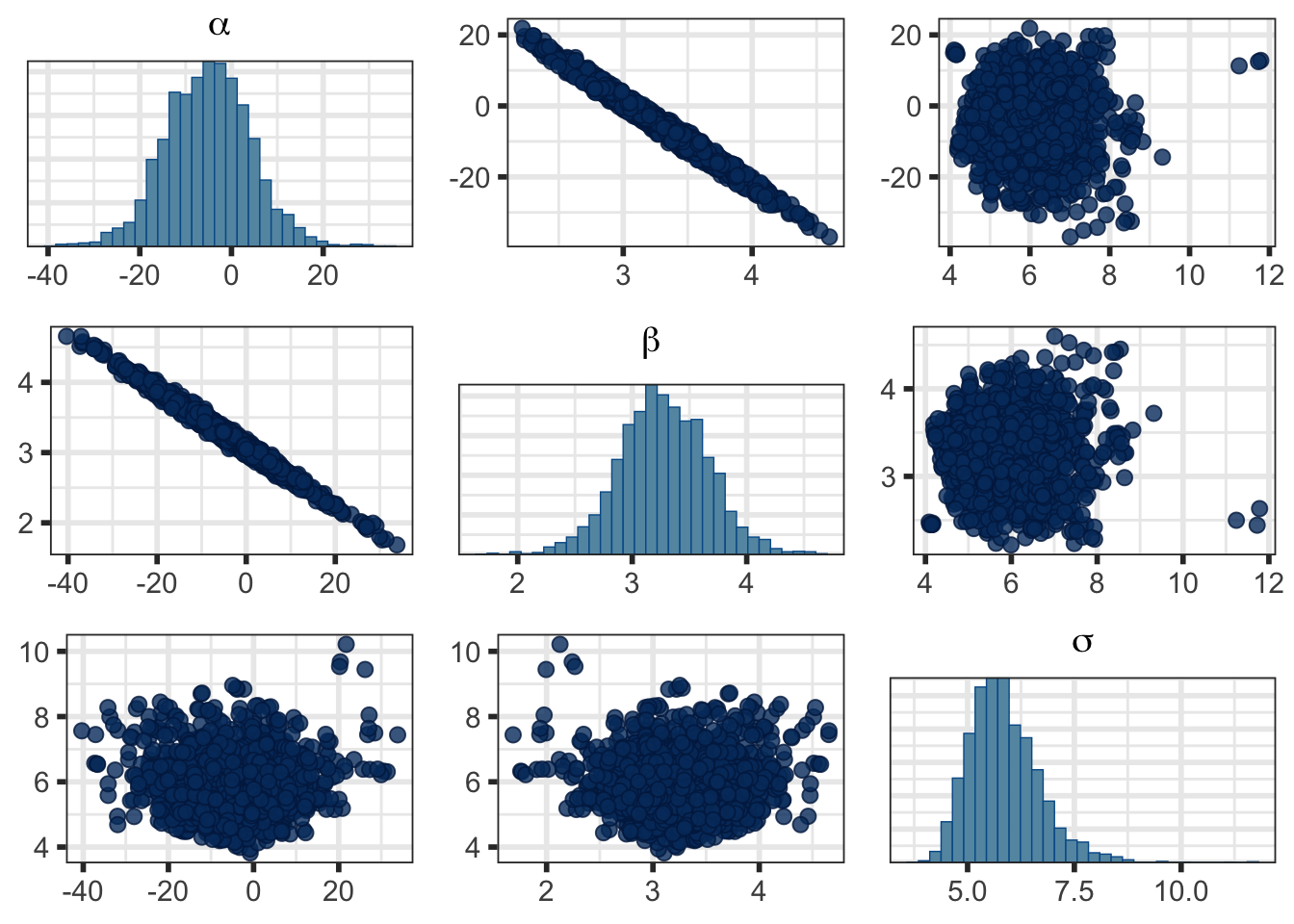

5.4 3-D Plots

Warning

3-D plots are generally considered bad practice, and I don’t particularly find 3-D plots all that useful - they’re just too hard to see and interpret, but you can make that decision for yourself.

You can also look at 3-dimensional plots1, although they’re not easy to interpret.

Code 
fig <- plot_ly(draws_df,
               x = ~alpha, y = ~beta, z = ~sigma) %>%
  add_markers(marker = list(opacity = 0.5,
                            size = 2)) %>%
  layout(scene = list(xaxis = list(title = 'alpha'),
                      yaxis = list(title = 'beta'),
                      zaxis = list(title = 'sigma')))


fig <- plot_ly(type = "scatter3d", mode = "markers") %>%
  add_trace(x = draws_df$alpha, y = draws_df$beta, z = draws_df$sigma,
            text = paste0("</br>\u03B1: ", draws_df$alpha, 
                          "</br>\u03B2: ", draws_df$beta, 
                          "</br>\u03C3: ", draws_df$sigma),
            hoverinfo = "text",
            marker = list(size = 2,
                          opacity = 0.5,
                          color = "blue")) %>%
  layout(title = "3D Joint Posterior",
         scene = list(xaxis = list(title = "\u03B1"),
                      yaxis = list(title = "\u03B2"),
                      zaxis = list(title = "\u03C3")))

fig
Figure 3: 3-dimensional plot of the posterior distribution

The main point of this is to show that we have a joint posterior that we can’t visualize when looking at only the basic marginal density and pairwise joint density plots.

5.5 Summary

The most basic idea of a posterior distribution is that it describes how likely a given combination of parameters is conditional on the data. For our example, a parameter combination \(\{\alpha, \beta, \sigma\} = \{-5, 3.2, 6\}\) seems to be fairly likely, \(\{-20, 4, 6\}\) is possible but less likely, and \(\{-20, 3.2, 6\}\) is for all intents and purposes impossible. While it is informative to look at numerical summaries and marginal and pairwise joint posteriors, we have to be go beyond these plots and summaries to get the bigger picture.

6 Posterior Predictions

In Section 5 we looked at the posterior distribution on the parameter scale. If we simulate data using draws from our posterior distribution, then we can visualize the posterior distribution on the data scale - this is precisely what we have done with y_pred_mean (posterior predicted means) and y_pred (posterior predictions = posterior predicted mean + error)2.

Since the posterior distribution weights each possible combination of \((\alpha, \beta, \sigma)\) based on how likely it is conditioned on the observed data, the predictions derived/simulated from these parameter combinations are also weighted based on how likely they are (conditioned on the observed data).

After collecting data, we have fit a model and sampled from the posterior (and posterior predictive) distribution. Now we can do some visualizations.

6.1 Posterior Predicted Mean

We’ll first look at the posterior predicted mean - basically \(p(\alpha + \beta \tilde{x} \; | \; y)\) for our grid of new \(\tilde{x}\) (x_pred) with varying levels of probability intervals:

Code 
preds_df <- draws_df %>%
  spread_draws(c(y_pred_mean, y_pred)[i]) %>% 
  ungroup() %>% 
  mutate(x_pred = stan_data$x_pred[i])

preds_df %>% 
  ggplot() +
  stat_lineribbon(aes(x = x_pred, y = y_pred_mean)) +
  geom_point(data = data,
             mapping = aes(x = x, y = y)) +
  scale_fill_brewer() +
  ylab("y") +
  xlab("x")

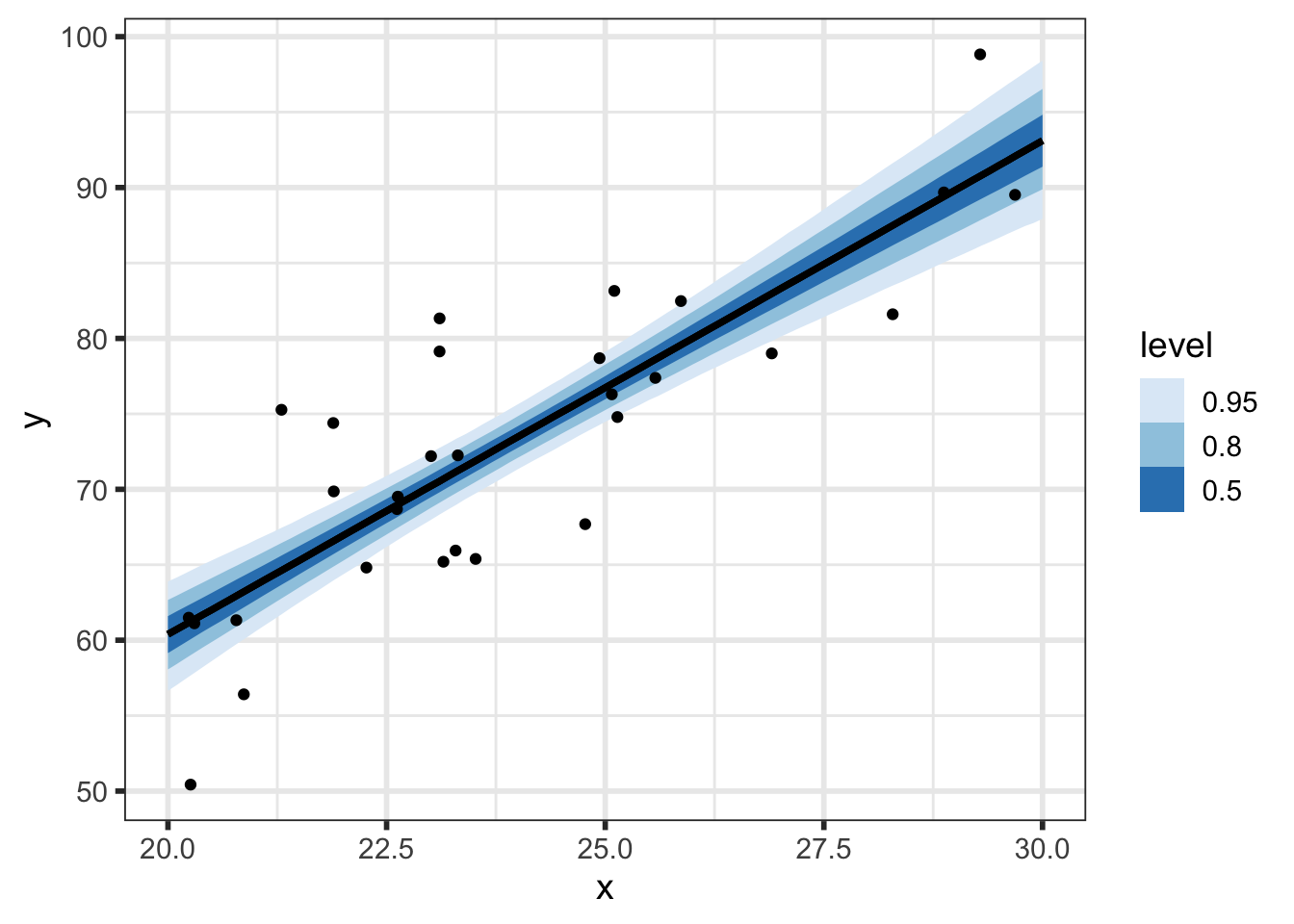
But we can do even better to visualize how our parameters relate to our predictions. We know that the \(i^{th}\) draw of parameters from the posterior, denoted \((\alpha^{[i]}, \beta^{[i]}, \sigma^{[i]})\), has been transformed to the data space by y_pred_mean\(\!^{[i]}=\alpha^{[i]} + \beta^{[i]}\tilde{x}\) and y_pred\(\!^{[i]}=\) y_pred_mean\(\!^{[i]} + \epsilon, \;\; \epsilon \sim N(0, \sigma^{[i]})\), so we now have draws of y_pred and y_pred_mean.

Code 
(p_pred_mean_spaghetti <- preds_df %>% 
  group_by(.chain) %>% 
  filter(.iteration <= 10) %>% 
  ggplot() +
  geom_line(aes(x = x_pred, y = y_pred_mean, group = .draw), color = "blue") +
  geom_point(data = data,
             mapping = aes(x = x, y = y)) +
  ylab("y") +
  xlab("x") +
  transition_states(.draw, 0, 1) +
  shadow_mark(future = TRUE, color = "gray50", alpha = 0.075))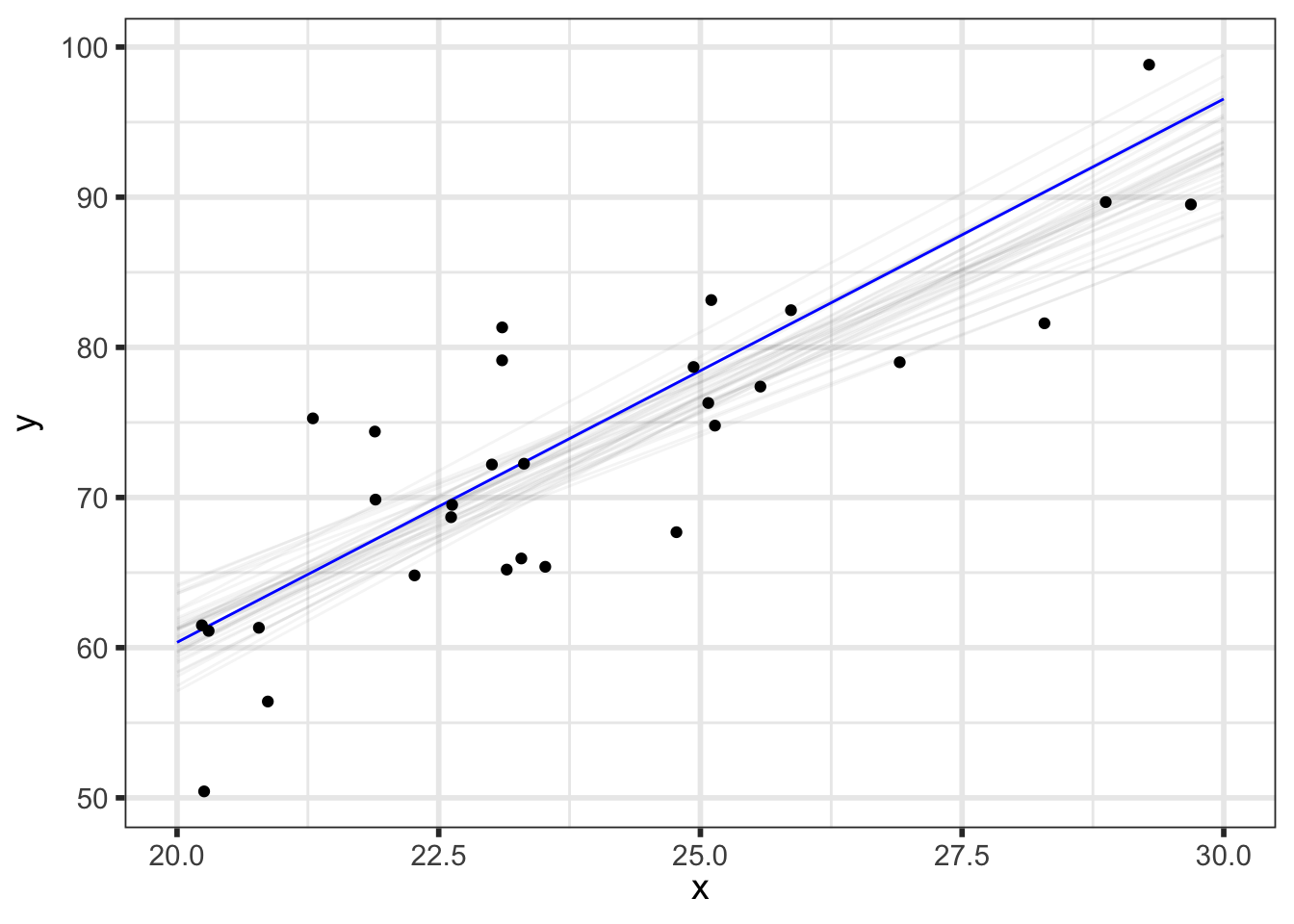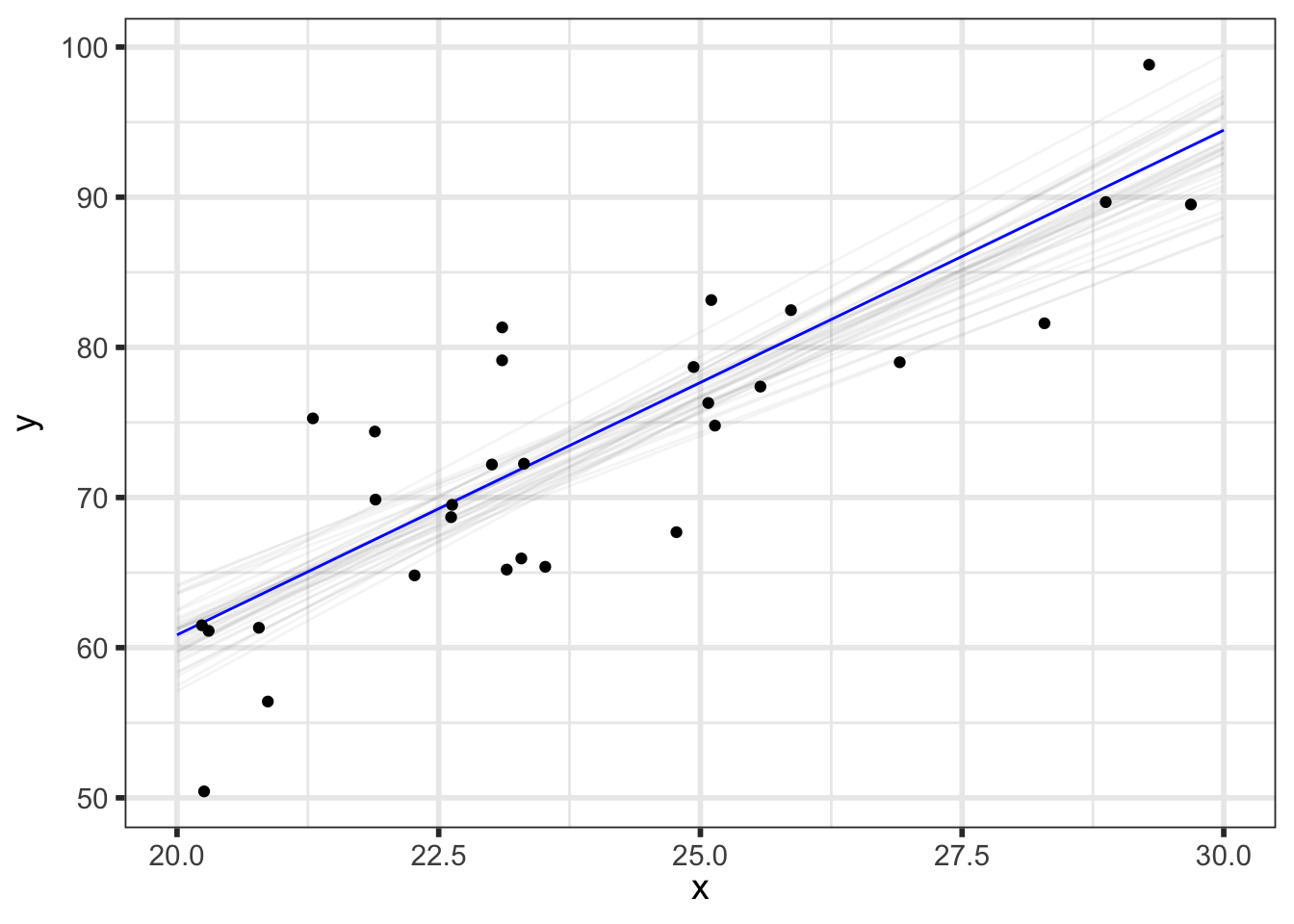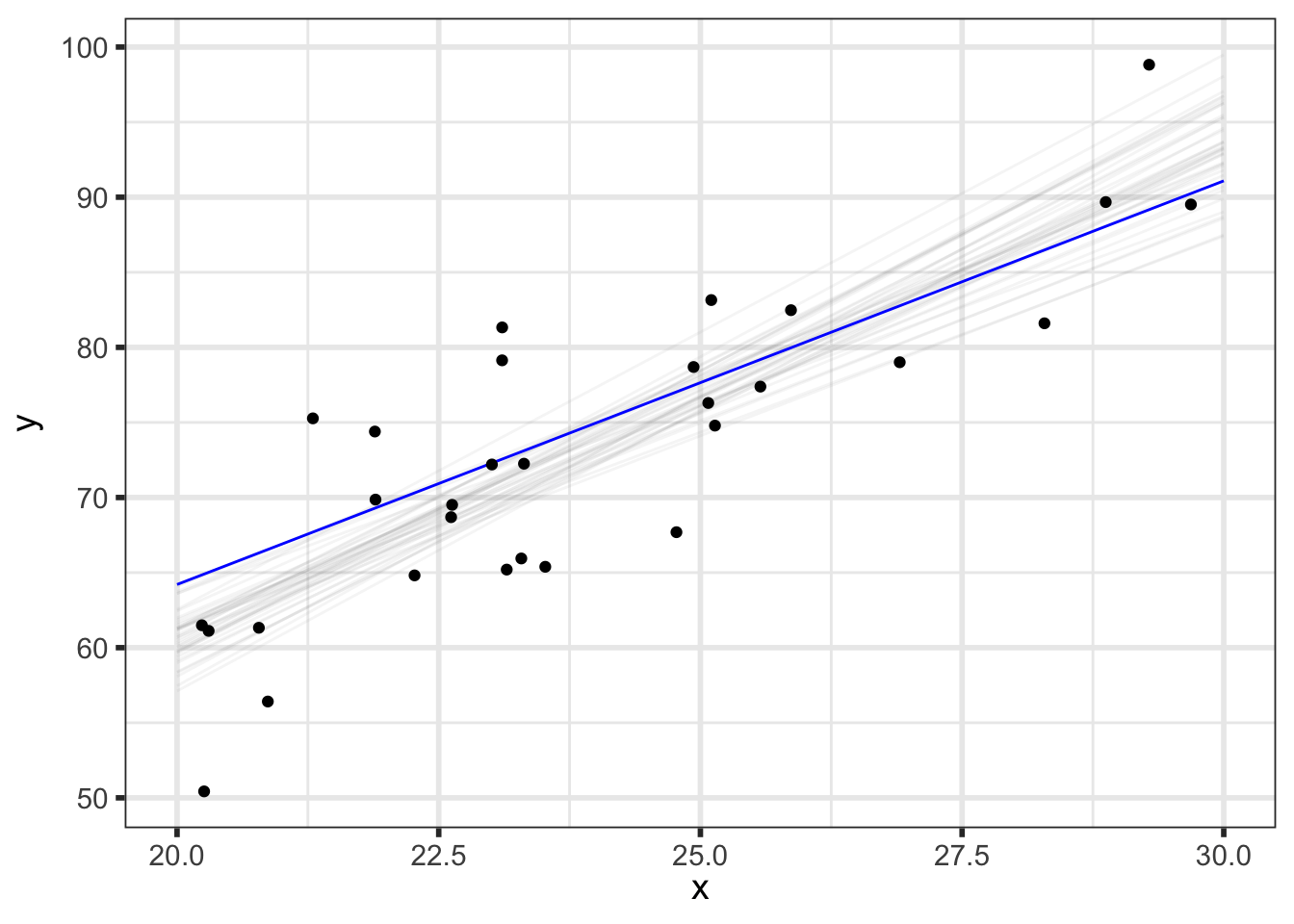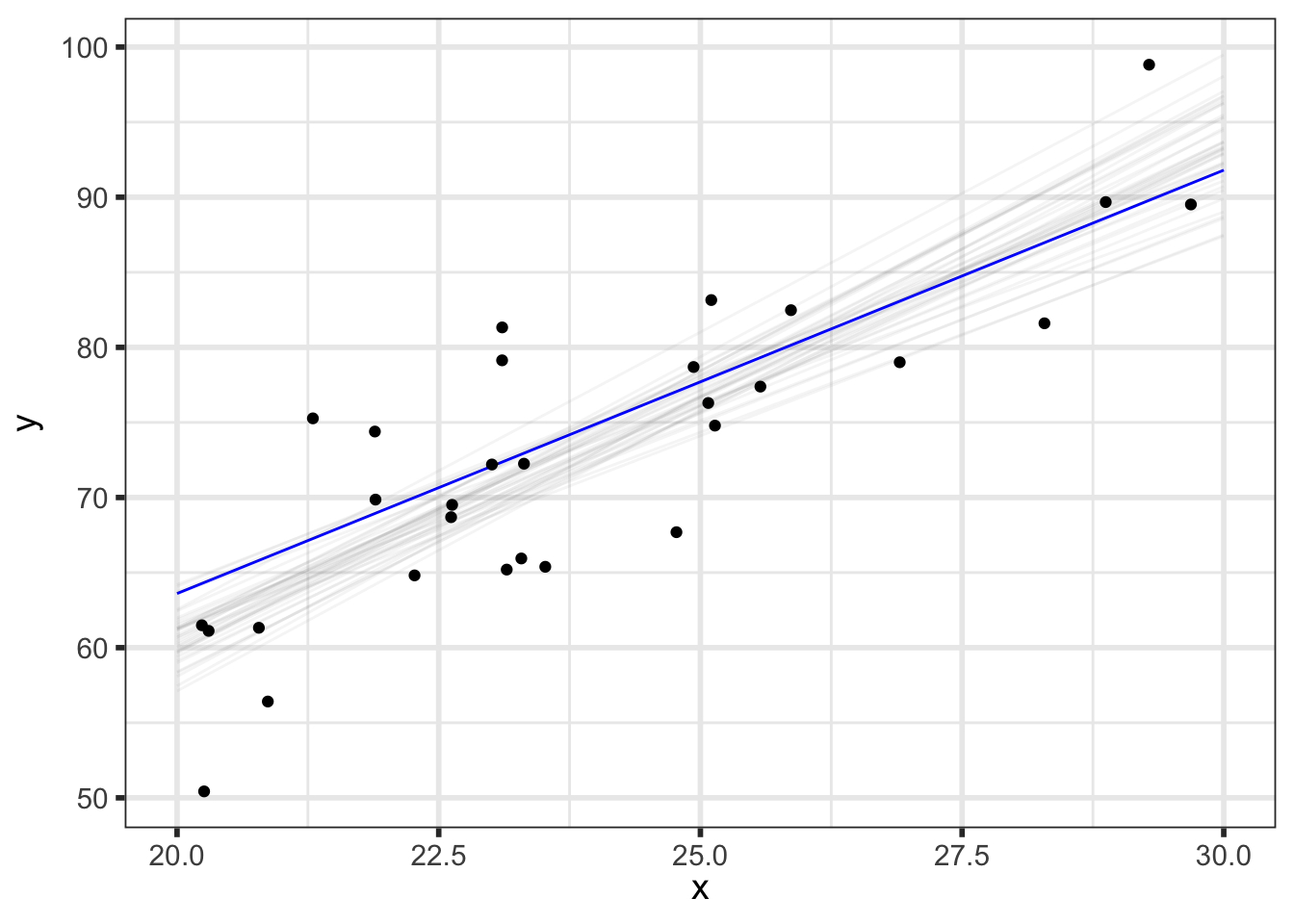
Figure 4: Highlighting each parameter draw to data space as predicted mean

7 Posterior Predictions

We can look at prediction intervals with varying levels of probability intervals:

Code 
preds_df %>% 
  ggplot() +
  stat_lineribbon(aes(x = x_pred, y = y_pred)) +
  geom_point(data = data,
             mapping = aes(x = x, y = y)) +
  scale_fill_brewer() +
  ylab("y") +
  xlab("x")
Figure 5

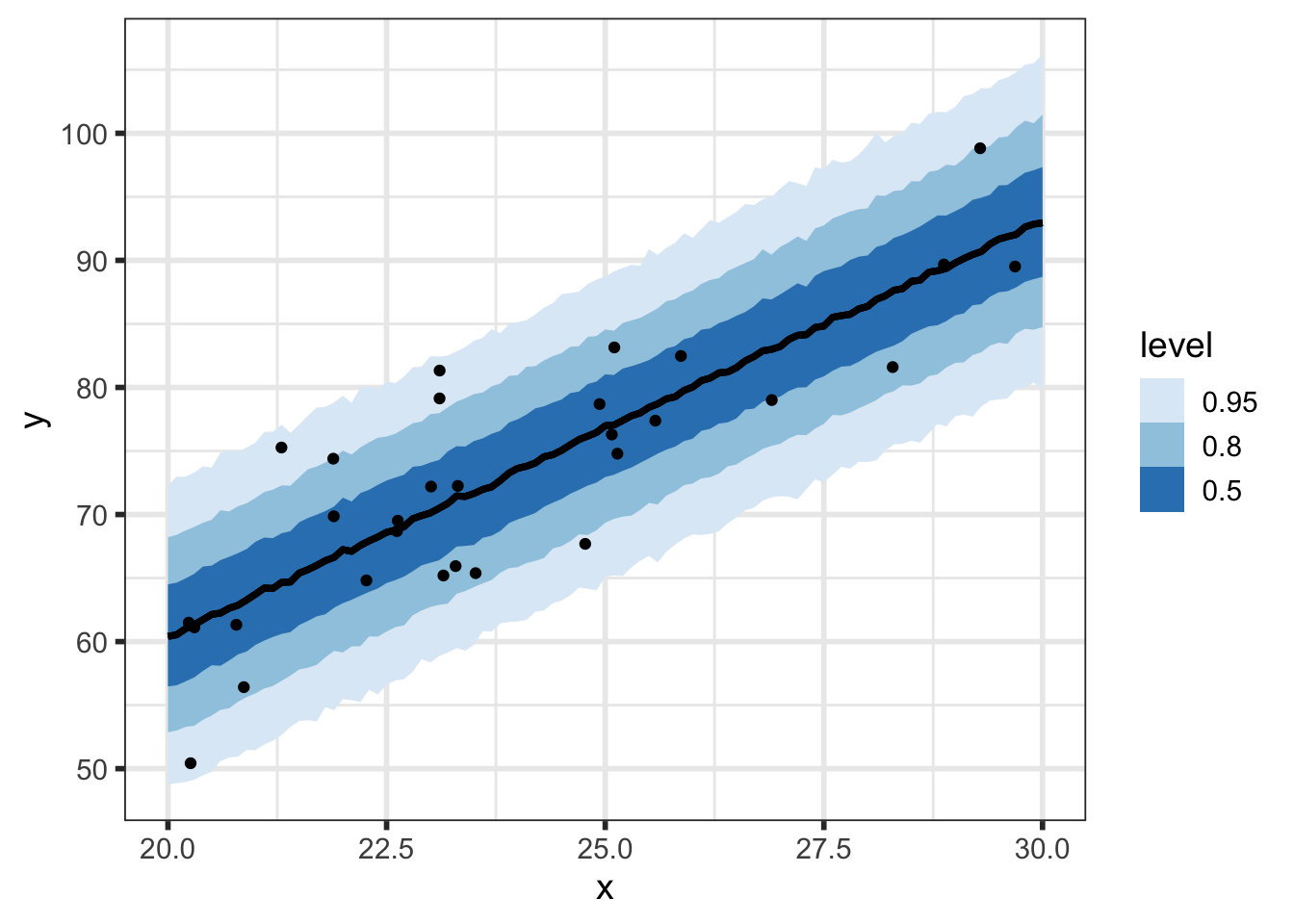
At every value of \(\tilde{x}\), we have a posterior predictive distribution. Here’s what that looks like for a select few values of \(\tilde{x}\):

Code 
{preds_df %>% 
  filter(x_pred %in% seq(20, 30, by = 2))} %>% 
  ggplot() +
  geom_line(. %>% 
              group_by(x_pred) %>% 
              summarize(mean = mean(y_pred_mean)),
            mapping = aes(x = x_pred, y = mean)) +
  stat_halfeye(aes(x = x_pred, y = y_pred, group = x_pred),
               scale = 0.5, interval_size = 2, .width = 0.95,
               point_interval = mean_qi, normalize = "xy",
               alpha = 0.2, fill = "blue") + 
  geom_point(data = data,
             mapping = aes(x = x, y = y)) +
  ylab("y") +
  xlab("x") +
  coord_cartesian(ylim = c(30, 120))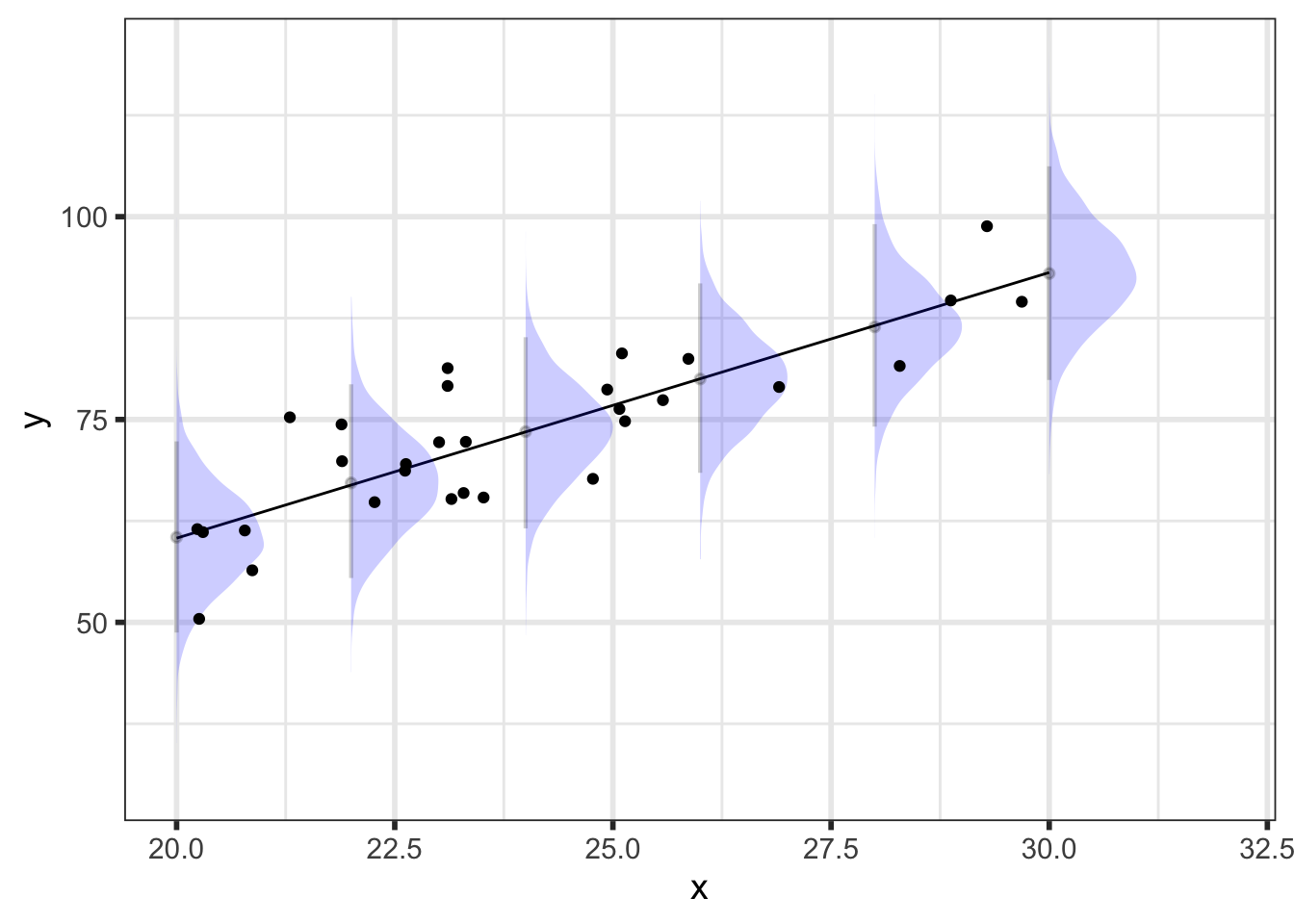

As an aside, this plot should illustrate the difference between the posterior predicted mean (red) and posterior predictions (blue) - the intervals are much bigger for the predictions to the addition of residual variability.

Code 
{preds_df %>% 
  filter(x_pred %in% seq(20, 30, by = 2))} %>% 
  ggplot() +
  geom_line(. %>% 
              group_by(x_pred) %>% 
              summarize(mean = mean(y_pred_mean)),
            mapping = aes(x = x_pred, y = mean)) +
  stat_halfeye(aes(x = x_pred, y = y_pred, group = x_pred),
               scale = 0.5, interval_size = 2, .width = 0.95,
               point_interval = mean_qi, normalize = "xy",
               alpha = 0.2, fill = "blue") + 
  stat_halfeye(aes(x = x_pred, y = y_pred_mean, group = x_pred),
               scale = 0.75, interval_size = 2, .width = 0.95,
               point_interval = mean_qi, normalize = "xy",
               alpha = 0.2, side = "left", fill = "red") +
  geom_point(data = data,
             mapping = aes(x = x, y = y)) +
  ylab("y") +
  xlab("x") +
  coord_cartesian(ylim = c(30, 120))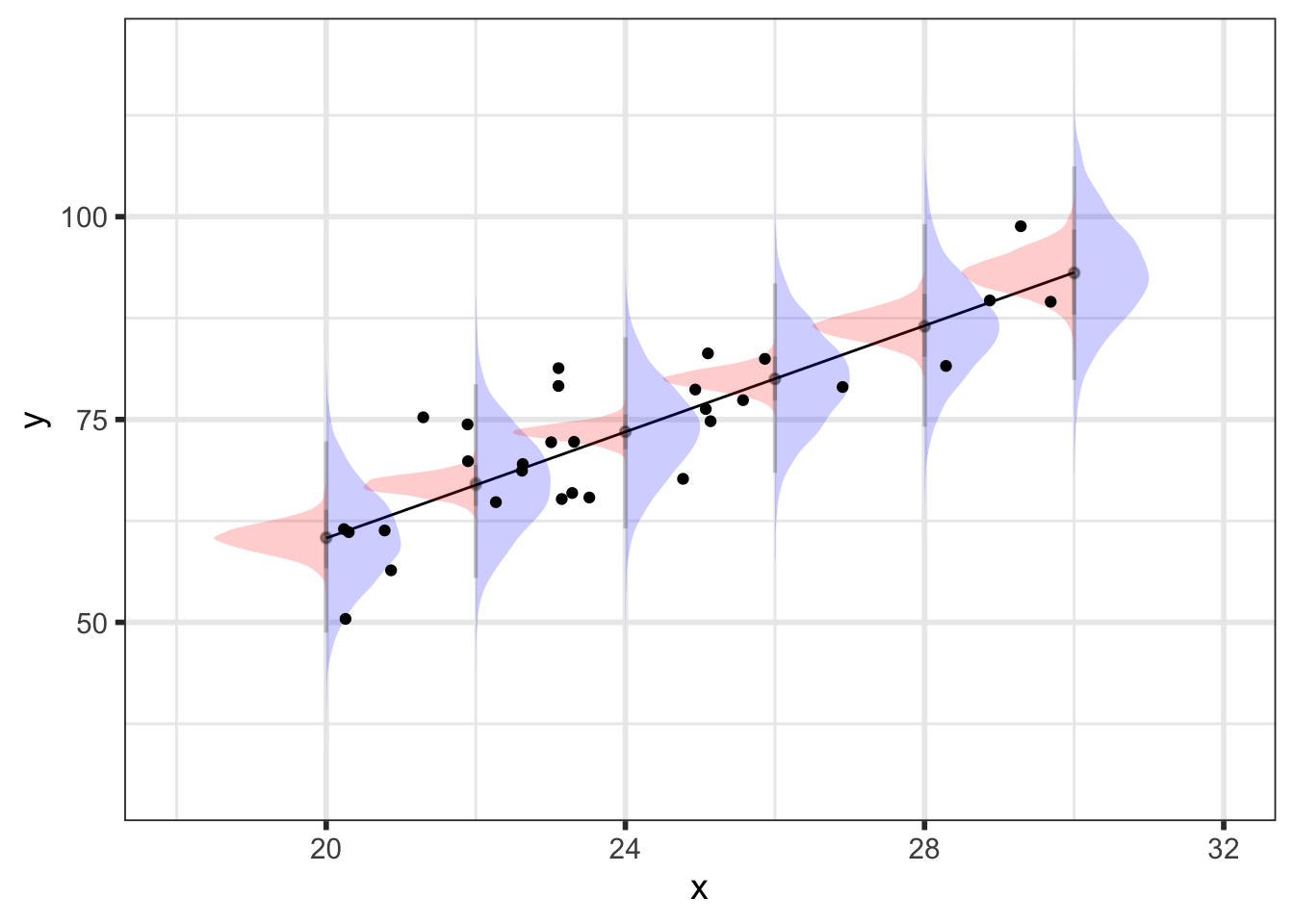

8 Summary

Hopefully this document gives you a bit more understanding of the posterior distribution and how it relates to posterior predictions.

Back to top

Footnotes

  1. This plot is interactive. Play around with it.↩︎

  2. And y_ppc. y_pred and y_ppc are distributed the same, except y_ppc are replicates of the data at observed values of \(x\), while y_pred are simulations at new values of \(x\), denoted \(\tilde{x}\) for the remainder of this document.↩︎