Fitting a Model

library(plotly)
library(gganimate)
library(knitr)
library(kableExtra)
library(tidybayes)
library(posterior)
library(bayesplot)
library(cmdstanr)
library(tidyverse)

register_knitr_engine(override = TRUE)
theme_set(theme_bw(base_size = 14, base_line_size = 1))

set_cmdstan_path("~/Torsten/cmdstan")

1 Torsten

Stan is not specialized for pharmacometrics, so it does not automatically handle dosing events and common models that pharmacometrics-specific software like NONMEM, Monolix, Pumas, and nlmixr do. These limitations are mitigated when Stan is used in conjunction with Torsten, a collection of Stan functions that are analogous to NONMEM’s ADVANs. Given a dataset that follows NONMEM’s NM-TRAN specifications, these functions specify common PMx models and do all the event handling required to fit (or simulate) pharmacometric data.

2 Data

Since we have the ability to fit standard NONMEM datasets, we can just read in a typical NONMEM-ready dataset that we get from our programming groups. It will then require a small amount of wrangling to get ready for Stan.

nonmem_data <- read_csv(here::here("Data/depot_1cmt_ppa_covariates.csv"),
                        na = ".") %>% 
  rename_all(tolower) %>% 
  rename(ID = "id",
         DV = "dv") %>% 
  mutate(DV = if_else(is.na(DV), 5555555, DV),    # This value can be anything except NA. It'll be indexed away 
         bloq = if_else(is.na(bloq), -999, bloq)) # This value can be anything except NA. It'll be indexed away

nonmem_data %>% 
  mutate(across(where(is.numeric), \(x) round(x, 3))) %>% 
  DT::datatable()

Table 1: NONMEM dataset

(p_1 <- ggplot(nonmem_data %>%
                 group_by(ID) %>%
                 mutate(Dose = factor(max(amt, na.rm = TRUE))) %>%
                 ungroup() %>%
                 filter(mdv == 0)) +
    geom_line(mapping = aes(x = time, y = DV, group = ID, color = Dose)) +
    geom_point(mapping = aes(x = time, y = DV, group = ID, color = Dose)) +
    scale_color_discrete(name = "Dose (mg)") +
    scale_y_continuous(name = latex2exp::TeX("$Drug\\;Conc.\\;(\\mu g/mL)$"),
                       limits = c(NA, NA),
                       trans = "log10") +
    scale_x_continuous(name = "Time (d)",
                       breaks = seq(0, 216, by = 24),
                       labels = seq(0, 216/24, by = 24/24),
                       limits = c(0, NA)) +
    theme_bw(18) +
    theme(axis.text = element_text(size = 14, face = "bold"),
          axis.title = element_text(size = 18, face = "bold"),
          axis.line = element_line(linewidth = 2),
          legend.position = "bottom"))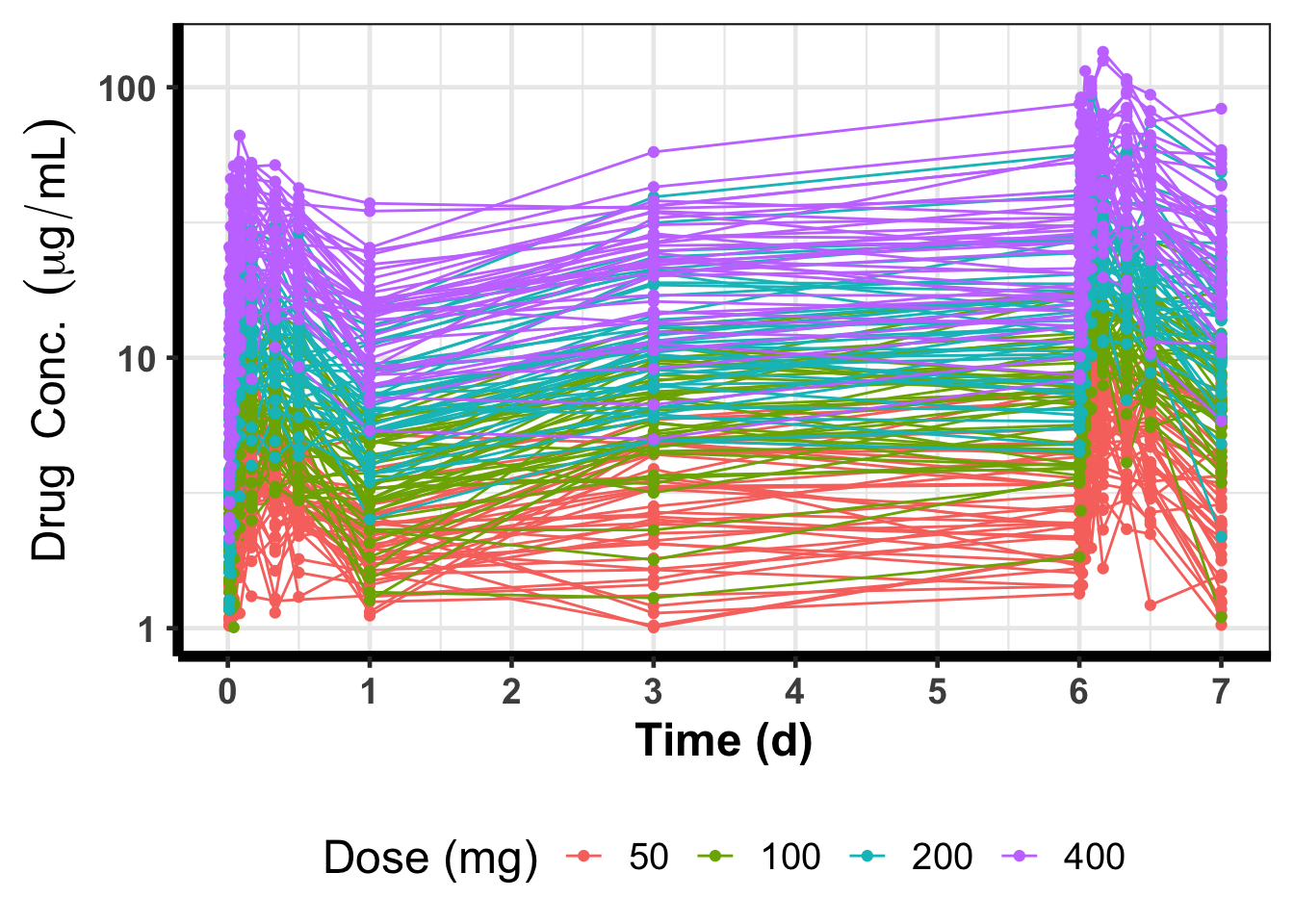

Figure 1

Then we need to wrangle the data to get it ready to be input into Stan:

n_subjects <- nonmem_data %>%  # number of individuals
  distinct(ID) %>%
  count() %>%
  deframe()

n_total <- nrow(nonmem_data)   # total number of records

i_obs <- nonmem_data %>%       # indices of the observations
  mutate(row_num = 1:n()) %>%
  filter(evid == 0) %>%
  select(row_num) %>%
  deframe()

n_obs <- length(i_obs)         # number of observations

subj_start <- nonmem_data %>%  # Indices that indicate which row is the start of a new subject
  mutate(row_num = 1:n()) %>%
  group_by(ID) %>%
  slice_head(n = 1) %>%
  ungroup() %>%
  select(row_num) %>%
  deframe()

subj_end <- c(subj_start[-1] - 1, n_total) # Indices that indicate which row is the end of a subject

# Covariates
wt <- nonmem_data %>% 
  group_by(ID) %>% 
  distinct(wt) %>% 
  ungroup() %>% 
  pull(wt)

cmppi <- nonmem_data %>% 
  group_by(ID) %>% 
  distinct(cmppi) %>% 
  ungroup() %>% 
  pull(cmppi)

egfr <- nonmem_data %>% 
  group_by(ID) %>% 
  distinct(egfr) %>% 
  ungroup() %>% 
  pull(egfr)

race <- nonmem_data %>% 
  group_by(ID) %>% 
  distinct(race) %>% 
  ungroup() %>% 
  pull(race)

n_races <- length(unique(race))

3 Model

Here’s the Stan model:

#| code-fold: false
// First Order Absorption (oral/subcutaneous)
// One-compartment PK Model
// IIV on CL, VC, and Ka (full covariance matrix)
// proportional plus additive error - DV = IPRED*(1 + eps_p) + eps_a
// Matrix-exponential solution using Torsten (the matrix-exponential seems to be
//   faster than the analytical solution for this model)
// Implements threading for within-chain parallelization 
// Deals with BLOQ values by the "CDF trick" (M4)
// Since we have a normal distribution on the error, but the DV must be > 0, it
//   truncates the likelihood below at 0
// For PPC, it generates values from a normal that is truncated below at 0
// Covariates: 
//   1) Body Weight on CL and VC - (wt/70)^theta
//   2) Concomitant administration of protein pump inhibitors (CMPPI) 
//      on KA (0/1) - exp(theta*cmppi)
//   3) eGFR on CL (continuous) - (eGFR/90)^theta
//   4) Race on VC - exp(theta_vc_{race}*I(race == {race}))

functions{
  
  int num_between(int lb, int ub, array[] int y){
    
    int n = 0;
    for(i in 1:num_elements(y)){
      if(y[i] >= lb && y[i] <= ub)
         n = n + 1;
    }
    return n;
    
  }
  
  array[] int find_between(int lb, int ub, array[] int y) {
    // vector[num_between(lb, ub, y)] result;
    array[num_between(lb, ub, y)] int result;
    int n = 1;
    for (i in 1:num_elements(y)) {
      if (y[i] >= lb && y[i] <= ub) {
        result[n] = y[i];
        n = n + 1;
      }
    }
    return result;
  }
  
  vector find_between_vec(int lb, int ub, array[] int idx, vector y) {
    
    vector[num_between(lb, ub, idx)] result;
    int n = 1;
    if(num_elements(idx) != num_elements(y)) reject("illegal input");
    for (i in 1:rows(y)) {
      if (idx[i] >= lb && idx[i] <= ub) {
        result[n] = y[i];
        n = n + 1;
      }
    }
    return result;
  }
  
  real normal_lb_rng(real mu, real sigma, real lb){
    
    real p_lb = normal_cdf(lb | mu, sigma);
    real u = uniform_rng(p_lb, 1);
    real y = mu + sigma * inv_Phi(u);
    return y; 

  }
  
  real partial_sum_lpmf(array[] int seq_subj, int start, int end,
                        vector dv_obs, array[] int dv_obs_id, array[] int i_obs,
                        array[] real amt, array[] int cmt, array[] int evid, 
                        array[] real time, array[] real rate, array[] real ii, 
                        array[] int addl, array[] int ss,
                        array[] int subj_start, array[] int subj_end, 
                        vector CL, vector VC, vector KA, 
                        real sigma_sq_p, real sigma_sq_a, real sigma_p_a,
                        vector lloq, array[] int bloq,
                        int n_random, int n_subjects, int n_total,
                        array[] real bioav, array[] real tlag, int n_cmt){
                           
    real ptarget = 0;
                              
    int N = end - start + 1;    // number of subjects in this slice  
    vector[n_total] dv_ipred;   
    matrix[n_total, 2] x_ipred;
  
    int n_obs_slice = num_between(subj_start[start], subj_end[end], i_obs);
    array[n_obs_slice] int i_obs_slice = find_between(subj_start[start], 
                                                      subj_end[end], i_obs);
                                                
    vector[n_obs_slice] dv_obs_slice = find_between_vec(start, end, 
                                                        dv_obs_id, dv_obs);
    
    vector[n_obs_slice] ipred_slice;
    
    vector[n_obs_slice] lloq_slice = lloq[i_obs_slice];
    array[n_obs_slice] int bloq_slice = bloq[i_obs_slice];
    
    
    for(n in 1:N){            // loop over subjects in this slice
    
      int j = n + start - 1; // j is the ID of the current subject
      

      matrix[n_cmt, n_cmt] K = rep_matrix(0, n_cmt, n_cmt);
      K[1, 1] = -KA[j];
      K[2, 1] = KA[j];
      K[2, 2] = -CL[j]/VC[j];
      
      x_ipred[subj_start[j]:subj_end[j], ] =
        pmx_solve_linode(time[subj_start[j]:subj_end[j]],
                         amt[subj_start[j]:subj_end[j]],
                         rate[subj_start[j]:subj_end[j]],
                         ii[subj_start[j]:subj_end[j]],
                         evid[subj_start[j]:subj_end[j]],
                         cmt[subj_start[j]:subj_end[j]],
                         addl[subj_start[j]:subj_end[j]],
                         ss[subj_start[j]:subj_end[j]],
                         K, bioav, tlag)';
                           
      dv_ipred[subj_start[j]:subj_end[j]] = 
        x_ipred[subj_start[j]:subj_end[j], 2] ./ VC[j];
    
    }
  
    ipred_slice = dv_ipred[i_obs_slice];
    
    for(i in 1:n_obs_slice){
      
      real ipred_tmp = ipred_slice[i];
      real sigma_tmp = sqrt(square(ipred_tmp) * sigma_sq_p + sigma_sq_a + 
                            2*ipred_tmp*sigma_p_a);
      
      if(bloq_slice[i] == 1){
        ptarget += log_diff_exp(normal_lcdf(lloq_slice[i] | ipred_tmp, 
                                                            sigma_tmp),
                                normal_lcdf(0.0 | ipred_tmp, sigma_tmp)) -
                   normal_lccdf(0.0 | ipred_tmp, sigma_tmp); 
      }else{
        ptarget += normal_lpdf(dv_obs_slice[i] | ipred_tmp, sigma_tmp) -
                   normal_lccdf(0.0 | ipred_tmp, sigma_tmp);
      }
    }                                         
                              
    return ptarget;
                           
  }
  
}
data{
  
  int n_subjects;
  int n_total;
  int n_obs;
  array[n_obs] int i_obs;
  array[n_total] int ID;
  array[n_total] real amt;
  array[n_total] int cmt;
  array[n_total] int evid;
  array[n_total] real rate;
  array[n_total] real ii;
  array[n_total] int addl;
  array[n_total] int ss;
  array[n_total] real time;
  vector<lower = 0>[n_total] dv;
  array[n_subjects] int subj_start;
  array[n_subjects] int subj_end;
  vector[n_total] lloq;
  array[n_total] int bloq;
  
  array[n_subjects] real<lower = 0> wt;                    // baseline bodyweight (kg)
  array[n_subjects] int<lower = 0, upper = 1> cmppi;       // cmppi
  array[n_subjects] real<lower = 0> egfr;                  // eGFR
  int<lower = 2> n_races;                                  // number of unique races
  array[n_subjects] int<lower = 1, upper = n_races> race;  // race
  
  real<lower = 0> location_tvcl;  // Prior Location parameter for CL
  real<lower = 0> location_tvvc;  // Prior Location parameter for VC
  real<lower = 0> location_tvka;  // Prior Location parameter for KA
  
  real<lower = 0> scale_tvcl;     // Prior Scale parameter for CL
  real<lower = 0> scale_tvvc;     // Prior Scale parameter for VC
  real<lower = 0> scale_tvka;     // Prior Scale parameter for KA
  
  real<lower = 0> scale_omega_cl; // Prior scale parameter for omega_cl
  real<lower = 0> scale_omega_vc; // Prior scale parameter for omega_vc
  real<lower = 0> scale_omega_ka; // Prior scale parameter for omega_ka
  
  real<lower = 0> lkj_df_omega;   // Prior degrees of freedom for omega cor mat
  
  real<lower = 0> scale_sigma_p;  // Prior Scale parameter for proportional error
  real<lower = 0> scale_sigma_a;  // Prior Scale parameter for additive error
  
  real<lower = 0> lkj_df_sigma;   // Prior degrees of freedom for sigma cor mat
  
  int<lower = 0, upper = 1> prior_only; // Want to simulate from the prior?
  int<lower = 0, upper = prior_only> no_gq_predictions; // Leave out PREDS and IPREDS in 
                                                        // generated quantities. Useful
                                                        // for simulating prior parameters
                                                        // but don't want prior predictions
 
}
transformed data{ 
  
  int grainsize = 1;
  
  vector<lower = 0>[n_obs] dv_obs = dv[i_obs];
  array[n_obs] int dv_obs_id = ID[i_obs];
  
  vector[n_obs] lloq_obs = lloq[i_obs];
  array[n_obs] int bloq_obs = bloq[i_obs];
  
  int n_random = 3;                    // Number of random effects
  int n_cmt = 2;                       // Number of states in the ODEs
  
  array[n_random] real scale_omega = {scale_omega_cl, scale_omega_vc, 
                                      scale_omega_ka}; 
                                      
  array[2] real scale_sigma = {scale_sigma_p, scale_sigma_a};
  
  array[n_subjects] int seq_subj = linspaced_int_array(n_subjects, 1, n_subjects); // reduce_sum over subjects
  
  array[n_cmt] real bioav = rep_array(1.0, n_cmt); // Hardcoding, but could be data or a parameter in another situation
  array[n_cmt] real tlag = rep_array(0.0, n_cmt);
  
}
parameters{ 
  
  real<lower = 0> TVCL;       
  real<lower = 0> TVVC; 
  real<lower = TVCL/TVVC> TVKA;
  
  real theta_cl_wt;
  real theta_vc_wt;
  real theta_ka_cmppi;
  real theta_cl_egfr;
  real theta_vc_race2;
  real theta_vc_race3;
  real theta_vc_race4;
  
  vector<lower = 0>[n_random] omega;
  cholesky_factor_corr[n_random] L;
  
  vector<lower = 0>[2] sigma;
  cholesky_factor_corr[2] L_Sigma;
  
  matrix[n_random, n_subjects] Z;
  
}
transformed parameters{
  
  vector[n_subjects] eta_cl;
  vector[n_subjects] eta_vc;
  vector[n_subjects] eta_ka;
  vector[n_subjects] CL;
  vector[n_subjects] VC;
  vector[n_subjects] KA;
  vector[n_subjects] KE;
  
  real<lower = 0> sigma_p = sigma[1];
  real<lower = 0> sigma_a = sigma[2];
  
  real<lower = 0> sigma_sq_p = square(sigma_p);
  real<lower = 0> sigma_sq_a = square(sigma_a);
  
  real cor_p_a;
  real sigma_p_a;

  {
  
    row_vector[n_random] typical_values = to_row_vector({TVCL, TVVC, TVKA});

    matrix[n_subjects, n_random] eta = diag_pre_multiply(omega, L * Z)';

    matrix[n_subjects, n_random] theta =
                          (rep_matrix(typical_values, n_subjects) .* exp(eta));
                          
    vector[n_races] theta_vc_race = [0, theta_vc_race2, theta_vc_race3, 
                                     theta_vc_race4]';
                                     
    matrix[2, 2] R_Sigma = multiply_lower_tri_self_transpose(L_Sigma);
    matrix[2, 2] Sigma = quad_form_diag(R_Sigma, sigma);
    
    eta_cl = col(eta, 1);
    eta_vc = col(eta, 2);
    eta_ka = col(eta, 3);
    
    cor_p_a = R_Sigma[1, 2];
    sigma_p_a = Sigma[1, 2];
    
    for(j in 1:n_subjects){
      
      real wt_over_70 = wt[j]/70;
      real wt_adjustment_cl = wt_over_70^theta_cl_wt;
      real wt_adjustment_vc = wt_over_70^theta_vc_wt;
      real cmppi_adjustment_ka = exp(theta_ka_cmppi*cmppi[j]);
      real egfr_adjustment_cl = (egfr[j]/90)^theta_cl_egfr;
      real race_adjustment_vc = exp(theta_vc_race[race[j]]);
      
      row_vector[n_random] theta_j = theta[j]; // access the parameters for subject j
      CL[j] = theta_j[1] * wt_adjustment_cl * egfr_adjustment_cl;
      VC[j] = theta_j[2] * wt_adjustment_vc * race_adjustment_vc;
      KA[j] = theta_j[3] * cmppi_adjustment_ka;
      KE[j] = CL[j]/VC[j];
      
    }
  
  }
  
}
model{ 
  
  // Priors
  TVCL ~ lognormal(log(location_tvcl), scale_tvcl);
  TVVC ~ lognormal(log(location_tvvc), scale_tvvc);
  TVKA ~ lognormal(log(location_tvka), scale_tvka) T[TVCL/TVVC, ];
  
  theta_cl_wt ~ std_normal();
  theta_vc_wt ~ std_normal();
  theta_ka_cmppi ~ std_normal();
  theta_cl_egfr ~ std_normal();
  theta_vc_race2 ~ std_normal();
  theta_vc_race3 ~ std_normal();
  theta_vc_race4 ~ std_normal();

  omega ~ normal(0, scale_omega);
  L ~ lkj_corr_cholesky(lkj_df_omega);
  
  sigma ~ normal(0, scale_sigma);
  L_Sigma ~ lkj_corr_cholesky(lkj_df_sigma);
  
  to_vector(Z) ~ std_normal();
  
  // Likelihood
  if(prior_only == 0){
    target += reduce_sum(partial_sum_lupmf, seq_subj, grainsize,
                         dv_obs, dv_obs_id, i_obs,
                         amt, cmt, evid, time, 
                         rate, ii, addl, ss, subj_start, subj_end, 
                         CL, VC, KA,
                         sigma_sq_p, sigma_sq_a, sigma_p_a, 
                         lloq, bloq,
                         n_random, n_subjects, n_total,
                         bioav, tlag, n_cmt);
  }
}
generated quantities{
  
  real<lower = 0> omega_cl = omega[1];
  real<lower = 0> omega_vc = omega[2];
  real<lower = 0> omega_ka = omega[3];

  real<lower = 0> omega_sq_cl = square(omega_cl);
  real<lower = 0> omega_sq_vc = square(omega_vc);
  real<lower = 0> omega_sq_ka = square(omega_ka);

  real cor_cl_vc;
  real cor_cl_ka;
  real cor_vc_ka;
  real omega_cl_vc;
  real omega_cl_ka;
  real omega_vc_ka;

  vector[no_gq_predictions ? 0 : n_obs] pred;
  vector[no_gq_predictions ? 0 : n_obs] epred_stan;
  vector[no_gq_predictions ? 0 : n_obs] ipred;
  vector[no_gq_predictions ? 0 : n_obs] epred;
  vector[no_gq_predictions ? 0 : n_obs] dv_ppc;
  vector[no_gq_predictions ? 0 : n_obs] log_lik;
  vector[no_gq_predictions ? 0 : n_obs] iwres;
 
  {
    
    matrix[n_random, n_random] R = multiply_lower_tri_self_transpose(L);
    matrix[n_random, n_random] Omega = quad_form_diag(R, omega);

    cor_cl_vc = R[1, 2];
    cor_cl_ka = R[1, 3];
    cor_vc_ka = R[2, 3];

    omega_cl_vc = Omega[1, 2];
    omega_cl_ka = Omega[1, 3];
    omega_vc_ka = Omega[2, 3];
    
  }
  
  if(no_gq_predictions == 0){
    
    vector[n_subjects] CL_new;
    vector[n_subjects] VC_new;
    vector[n_subjects] KA_new;
    vector[n_subjects] KE_new;
    
    vector[n_total] dv_pred;
    matrix[n_total, n_cmt] x_pred;
    vector[n_total] dv_epred;
    matrix[n_total, n_cmt] x_epred;
    vector[n_total] dv_ipred;
    matrix[n_total, n_cmt] x_ipred;
    
    matrix[n_subjects, n_random] eta_new;
    matrix[n_subjects, n_random] theta_new;
    
    vector[n_races] theta_vc_race = [0, theta_vc_race2, theta_vc_race3, 
                                     theta_vc_race4]';
    
    for(i in 1:n_subjects){
      eta_new[i, ] = multi_normal_cholesky_rng(rep_vector(0, n_random),
                                               diag_pre_multiply(omega, L))';
    }
    theta_new = (rep_matrix(to_row_vector({TVCL, TVVC, TVKA}), n_subjects) .* exp(eta_new));

    for(j in 1:n_subjects){
    
      real wt_over_70 = wt[j]/70;
      real wt_adjustment_cl = wt_over_70^theta_cl_wt;
      real wt_adjustment_vc = wt_over_70^theta_vc_wt;
      real cmppi_adjustment_ka = exp(theta_ka_cmppi*cmppi[j]);
      real egfr_adjustment_cl = (egfr[j]/90)^theta_cl_egfr;
      real race_adjustment_vc = exp(theta_vc_race[race[j]]);
      
      row_vector[n_random] theta_j_new = theta_new[j]; // access the parameters for subject j
      CL_new[j] = theta_j_new[1] * wt_adjustment_cl * egfr_adjustment_cl;
      VC_new[j] = theta_j_new[2] * wt_adjustment_vc * race_adjustment_vc;
      KA_new[j] = theta_j_new[3] * cmppi_adjustment_ka;
      KE_new[j] = CL_new[j]/VC_new[j];
      
      real cl_p = TVCL * wt_adjustment_cl * egfr_adjustment_cl;
      real vc_p = TVVC * wt_adjustment_vc * race_adjustment_vc;
      real ka_p = TVKA * cmppi_adjustment_ka;
    
      matrix[n_cmt, n_cmt] K = rep_matrix(0, n_cmt, n_cmt);
      matrix[n_cmt, n_cmt] K_epred = rep_matrix(0, n_cmt, n_cmt);
      matrix[n_cmt, n_cmt] K_p = rep_matrix(0, n_cmt, n_cmt);
      
      K[1, 1] = -KA[j];
      K[2, 1] = KA[j];
      K[2, 2] = -KE[j];
      
      x_ipred[subj_start[j]:subj_end[j], ] =
        pmx_solve_linode(time[subj_start[j]:subj_end[j]],
                         amt[subj_start[j]:subj_end[j]],
                         rate[subj_start[j]:subj_end[j]],
                         ii[subj_start[j]:subj_end[j]],
                         evid[subj_start[j]:subj_end[j]],
                         cmt[subj_start[j]:subj_end[j]],
                         addl[subj_start[j]:subj_end[j]],
                         ss[subj_start[j]:subj_end[j]],
                         K, bioav, tlag)';
                         
      K_epred[1, 1] = -KA_new[j];
      K_epred[2, 1] = KA_new[j];
      K_epred[2, 2] = -KE_new[j];
      
      x_epred[subj_start[j]:subj_end[j], ] =
        pmx_solve_linode(time[subj_start[j]:subj_end[j]],
                         amt[subj_start[j]:subj_end[j]],
                         rate[subj_start[j]:subj_end[j]],
                         ii[subj_start[j]:subj_end[j]],
                         evid[subj_start[j]:subj_end[j]],
                         cmt[subj_start[j]:subj_end[j]],
                         addl[subj_start[j]:subj_end[j]],
                         ss[subj_start[j]:subj_end[j]],
                         K_epred, bioav, tlag)';
                         
      K_p[1, 1] = -ka_p;
      K_p[2, 1] = ka_p;
      K_p[2, 2] = -cl_p/vc_p;

      x_pred[subj_start[j]:subj_end[j],] =
        pmx_solve_linode(time[subj_start[j]:subj_end[j]],
                         amt[subj_start[j]:subj_end[j]],
                         rate[subj_start[j]:subj_end[j]],
                         ii[subj_start[j]:subj_end[j]],
                         evid[subj_start[j]:subj_end[j]],
                         cmt[subj_start[j]:subj_end[j]],
                         addl[subj_start[j]:subj_end[j]],
                         ss[subj_start[j]:subj_end[j]],
                         K_p, bioav, tlag)';
      
      dv_ipred[subj_start[j]:subj_end[j]] =
        x_ipred[subj_start[j]:subj_end[j], 2] ./ VC[j];
        
      dv_epred[subj_start[j]:subj_end[j]] =
        x_epred[subj_start[j]:subj_end[j], 2] ./ VC_new[j];
      
      dv_pred[subj_start[j]:subj_end[j]] =
        x_pred[subj_start[j]:subj_end[j], 2] ./ vc_p;
      
    }

    pred = dv_pred[i_obs];
    epred_stan = dv_epred[i_obs];
    ipred = dv_ipred[i_obs];

    for(i in 1:n_obs){
      real ipred_tmp = ipred[i];
      real sigma_tmp = sqrt(square(ipred_tmp) * sigma_sq_p + sigma_sq_a + 
                            2*ipred_tmp*sigma_p_a);
      real epred_tmp = epred_stan[i];
      real sigma_tmp_e = sqrt(square(epred_tmp) * sigma_sq_p + sigma_sq_a + 
                              2*epred_tmp*sigma_p_a);
      dv_ppc[i] = normal_lb_rng(ipred_tmp, sigma_tmp, 0.0);
      epred[i] = normal_lb_rng(epred_tmp, sigma_tmp_e, 0.0);
      if(bloq_obs[i] == 1){
        // log_lik[i] = log(normal_cdf(lloq_obs[i] | ipred_tmp, sigma_tmp) -
        //                  normal_cdf(0.0 | ipred_tmp, sigma_tmp)) -
        //              normal_lccdf(0.0 | ipred_tmp, sigma_tmp);
        log_lik[i] = log_diff_exp(normal_lcdf(lloq_obs[i] | ipred_tmp, sigma_tmp),
                                  normal_lcdf(0.0 | ipred_tmp, sigma_tmp)) -
                     normal_lccdf(0.0 | ipred_tmp, sigma_tmp);
      }else{
        log_lik[i] = normal_lpdf(dv_obs[i] | ipred_tmp, sigma_tmp) -
                     normal_lccdf(0.0 | ipred_tmp, sigma_tmp);
      }
      iwres[i] = (dv_obs[i] - ipred_tmp)/sigma_tmp;
    }
  }
}

4 Fit and Save Fitted Object

model <- cmdstan_model(here::here("Stan/Fit/depot_1cmt_ppa_covariates.stan"),
                       cpp_options = list(stan_threads = TRUE))

stan_data <- list(n_subjects = n_subjects,
                  n_total = n_total,
                  n_obs = n_obs,
                  i_obs = i_obs,
                  ID = nonmem_data$ID,
                  amt = nonmem_data$amt,
                  cmt = nonmem_data$cmt,
                  evid = nonmem_data$evid,
                  rate = nonmem_data$rate,
                  ii = nonmem_data$ii,
                  addl = nonmem_data$addl,
                  ss = nonmem_data$ss,
                  time = nonmem_data$time,
                  dv = nonmem_data$DV,
                  subj_start = subj_start,
                  subj_end = subj_end,
                  wt = wt,
                  cmppi = cmppi,
                  egfr = egfr,
                  n_races = n_races,
                  race = race,
                  lloq = nonmem_data$lloq,
                  bloq = nonmem_data$bloq,
                  location_tvcl = 0.5,
                  location_tvvc = 4,
                  location_tvka = 0.8,
                  scale_tvcl = 1,
                  scale_tvvc = 1,
                  scale_tvka = 1,
                  scale_omega_cl = 0.4,
                  scale_omega_vc = 0.4,
                  scale_omega_ka = 0.4,
                  lkj_df_omega = 2,
                  scale_sigma_p = 0.5,
                  scale_sigma_a = 0.5,
                  lkj_df_sigma = 2,
                  prior_only = 0,
                  no_gq_predictions = 0) 

fit <- model$sample(data = stan_data,
                    seed = 112358,
                    chains = 4,
                    parallel_chains = 4,
                    threads_per_chain = parallel::detectCores()/4,
                    iter_warmup = 500,
                    iter_sampling = 1000,
                    adapt_delta = 0.8,
                    refresh = 500,
                    max_treedepth = 10,
                    # output_dir = "depot_1cmt_linear_covariates/Stan/Fits/Output",
                    # output_basename = "ppa_covariates",
                    init = function() list(TVCL = rlnorm(1, log(1), 0.3),
                                           TVVC = rlnorm(1, log(8), 0.3),
                                           TVKA = rlnorm(1, log(0.8), 0.3),
                                           theta_cl_wt = rnorm(1, 0, 0.2),
                                           theta_vc_wt = rnorm(1, 0, 0.2),
                                           theta_ka_cmppi = rnorm(1, 0, 0.2),
                                           theta_cl_egfr = rnorm(1, 0, 0.2),
                                           theta_vc_race2 = rnorm(1, 0, 0.2),
                                           theta_vc_race3 = rnorm(1, 0, 0.2),
                                           theta_vc_race4 = rnorm(1, 0, 0.2),
                                           omega = rlnorm(3, log(0.3), 0.3),
                                           sigma = rlnorm(2, log(0.2), 0.3)))

fit$save_object(
  "Stan/Fits/depot_1cmt_ppa_covariates.rds")

fit$save_data_file(dir = "Stan/Fits/Stan_Data",
                   basename = "ppa_covariates", timestamp = FALSE, 
                   random = FALSE)